5.7 Diseño de observadores

 5.7 Diseño de observadores

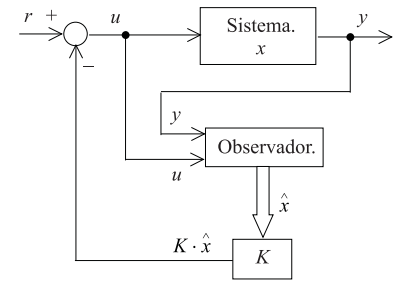
Un observador de estados es un sistema dinámico cuyos estados convergen a los del sistema observado. Dependiendo del numero de estados observados, el observador es de orden completo o reducido. Luego puede implementarse un control con asignación de autovalores de lazo cerrado por realimentación de los estados observados

Observador de Orden completo    
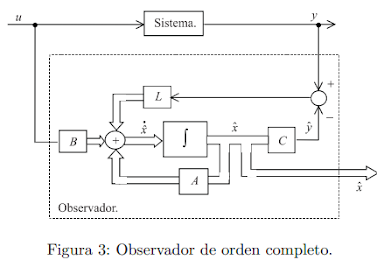
Consideremos que se desea estimar los estados x de un sistema lineal

siendo las matrices A, B y C son conocidas. Se propone la siguiente estructura genérica para el observador

donde las matrices Ao y L deben ser diseñadas para cumplir el objetivo de forzar la convergencia de los estados del observador a los del sistema. Por otra parte, z es una señal a determinar, si bien aun no es conocida es razonable pensar que dependa de la excitación u del sistema a observar. La dinámica del error definido por la diferencia entre los estados del sistema y los estados del observador resulta de la diferencia entre las ecuaciones:
Para asegurar que el error e = x − x converja a cero, mas allá de la excitación u del sistema, de su salida y y del valor inicial del error e(0), la ecuación debería poder reducirse a:
donde los autovalores de la matriz A˜ deben pertenecer al semiplano izquierdo. Esta reducción es posible si:
Luego el diseño del observador se reduce a encontrar una matriz L que asigne sus autovalores en:
  1. El semiplano izquierdo, lo cual asegura la estabilidad del observador, 
  2. Y a la izquierda de los autovalores del sistema para asegurar que la dinámica del error e = Aoe sea más rápida que la del sistema. ¿Por que?
La figura muestra un diagrama en bloques del conjunto sistema-observador. Para obtener la Fig. 3 se han realizado transformaciones elementales, obteniéndose así, el diagrama en bloques que puede encontrarse en muchos libros de texto (cuya interpretación física resulta inmediata)






Referencias
  • Ogata, K. (1996). Sistemas de control en tiempo discreto. Pearson educación.
  • Giraldo, D., & Giraldo, E. (2007). Control por realimentación de variables de estado usando un observador adaptativo de estados. Scientia et technica, 1(35).








Comentarios

Publicar un comentario

Entradas más populares de este blog

4.2 Criterio de estabilidad por Bode (Margen de ganancias y fase)

Imagen
Criterio de Estabilidad de Bode A continuación se indican las condiciones de estabilidad: Para el sistema estable: Ambos márgenes deben ser positivos o el margen de fase debe ser mayor que el margen de ganancia. Para el Sistema Marginal Estable: Ambos márgenes deben ser cero o el margen de fase debe ser igual al margen de ganancia. Para el Sistema Inestable: Si alguno de ellos es negativo o margen de fase debería ser menor que el margen de ganancia. Ganancia de margen Cuanto mayor sea el Ganancia de margen (GM), mayor será la estabilidad del sistema. El margen de ganancia se refiere a la cantidad de ganancia, la cual puede ser aumentada o disminuida sin hacer el sistema inestable. Se suele expresar como una magnitud en dB. Por lo general, podemos leer el margen de ganancia directamente del gráfico de Bode (como se muestra en el diagrama anterior). Esto se hace calculando la distancia vertical entre la curva de magnitud (en el gráfico de magnitud de Bode) y el eje x en la frecuencia don...
Leer más

2.3 Concepto de polos y ceros y su efecto en la respuesta del sistema.

Imagen
 Polos y ceros de una función de transferencia.  G(s) = Salida / Entrada = Q(S) / P(s)                          G(s)= Polinomio salida / Polinomio entrada La función de transferencia G(s) de un sistema lineal invariante en el tiempo, puede expresarse como el cociente de dos polinomios en "s". Si ahora se expresa a G(s) como el producto de los factores lineales que incluyen a esas raices, la ecuación se convierte en:    Entonces, ¿Qué son los ceros en un sistema? El valor(es) para  z   donde el  numerador  de la función de trasferencia es igual a cero Las frecuencias complejas que hacen que la ganancia de la función de transferencia del filtro sea cero. En cuanto a los ceros, suele decirse que, si el sistema es excitado con una señal que contenga la frecuencia de alguno de los ceros, la salida será nula. Sin embargo, esto no es completamente cierto ya que la s...
Leer más

3.2 TIPOS DE CONTROLADORES (P , PI Y PID)

Imagen
3.2  TIPOS DE CONTROLADORES P,  PI  Y  PID Introducción En este capítulo veremos la familia de controladores PID, que mostraron ser robustos en muchas aplicaciones y son los que más se utilizan en la industria. La estructura de un controlador PID es simple, aunque su simpleza es también su debilidad, dado que limita el rango de plantas donde pueden controlar en forma satisfactoria (existe un grupo de plantas inestables que no pueden estabilizadas con ningún miembro de la familia PID). En este capítulo estudiaremos los enfoques tradicionales al diseño de controladores PID. Estructura del PID Consideremos un lazo de control de una entrada y una salida (SISO) de un grado de libertad Los miembros de la familia de controladores PID, incluyen tres acciones: proporcional (P), integral (I) y derivativa (D). Estos controladores son los denominados P, I, PI, PD y PID. • P acción de control proporcional,  ...
Leer más