2.4 Análisis de la respuesta de un sistema
Respuesta transitoria
La respuesta transitoria de un sistema para una entrada escalón unitario depende de las condiciones iniciales. Por conveniencia al comparar respuestas transitorias de varios sistemas, es una práctica común usar la condición inicial estándar de que el sistema está en reposo al inicio, por lo cual la salida y todas las derivadas con respecto al tiempo son cero. De este modo, las características de respuesta se comparan con facilidad.
La respuesta transitoria de un sistema de control práctico exhibe con frecuencia oscilaciones amortiguadas antes de alcanzar el estado estable. Al especificar las características de la respuesta transitoria de un sistema de control para una entrada escalón unitario
sistemas de primer orden
Un sistema de primer orden sin ceros puede ser descrito por la función de transferencia que se muestra en la figura (1), se muestra la ubicación del polo en el plano complejo S. A continuación se mostrará la relación que existe entre la respuesta del sistema y la ubicación de los polos en el plano complejo de los sistemas de primer orden.
donde k y τ son la ganancia del sistema y la constante de tiempo respectivamente.
Respuesta a la rampa
La respuesta de un sistema de primer orden representado por su función de transferencia
Respuesta al impulso
Para una entrada impulso unitario δ(t), la salida del sistema es:
La transformada inversa de Laplace es
En el análisis anterior, se demostró que la respuesta del sistema y(t) ante una entrada rampa unitaria es dada por la ecuación.
Es la parte de la respuesta total que permanece después de que la respuesta transitoria ha desaparecido. Por lo tanto, está relacionada con la precisión del sistema definida por las constantes de error de posición Ep (a una entrada escalón) y error de velocidad Ev (a una entrada rampa).
Características de la respuesta en estado estable
Una característica importante de funcionamiento de los sistemas de control en estado estable, se refiere al error que presentan dichos sistemas en régimen permanente. Este error es una medida de la precisión de un sistema de control.
Para un sistema como el mostrado en la figura, se definen las siguientes señales de error:
E(s) = R(s) - C(s) señal de error
Ea(s) = R(s) - H(s)C(s) señal de error actuante
La expresión del error actuante Ea(s) en función de la excitación es:
El error actuante del sistema en estado estacionario se define como el valor del error actuante ea(t) cuando la respuesta ha adquirido su valor estacionario, esto es:










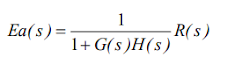




Comentarios
Publicar un comentario